[Index]

|
4. Understanding the formulas--Page 4
Using the Sum and Difference formulas, we can easily get the Derived formulas.
![]() ,
if k
is an odd integer,
,
if k
is an odd integer,
![]() ,
if k
is an even integer.
,
if k
is an even integer.
Here T can be any trigonometric functions, and co-T is the co-function of function T. For example, sine and cosine are co-functions of each other, similarly tangent and cotangent, secant and cosecant respectively.
For example
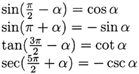
and so on, all of such formulas can proved by the Sum and Difference formulas:
![]() ,
,
since ![]() .
.
![]()
since ![]() , and so on. In the same way we can prove all of them.
, and so on. In the same way we can prove all of them.

