[Index]

|
5. Summarizing the formulas
The key to verifying identities is very good formula usage. Besides good memorization and understanding of all formulas, we need to summarize the actions of formulas. In our minds, we must clearly know what we can do, what we can't do. For examples, we have four Sum-to-Product formulas:
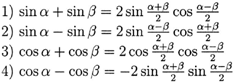
What characteristics do the formulas have? We see that any sum
can become a product, if the functions of two angles are the same,
(both are sines or cosines)
and with the same coefficients 1. The questions are: can we
make a sum into a product, if (1) the functions of two angles
are not the same, for example: ![]() ,
or (2) the coefficients of
,
or (2) the coefficients of ![]() are not 1, but still are the same, for example:
are not 1, but still are the same, for example: ![]() ,
or (3) if the coefficients are not the same, for example:
,
or (3) if the coefficients are not the same, for example: ![]() .
.
The answer of first question is yes. In fact, we can use the Derived
formula ![]() to exchange with one function so that the two functions are
to be the same. Then using the first one of the four Sum-to-Product
formulas, we have
to exchange with one function so that the two functions are
to be the same. Then using the first one of the four Sum-to-Product
formulas, we have

which reaches the goal from sum to product.
The answer of second question is yes. We have
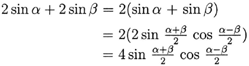
After factoring the same coefficient, the form in parentheses is exactly the form of the Sum to Product formulas. By using formulas, we have realized the goal of sum to product.

