[Index]
 |
2. What is the essence of verifying an identity?
The purpose of verifying an identity is to prove that the two sides of the equation are equal. If the two sides are the same, we need to verify nothing. When an identity needs to be proved, the two sides of the equal sign have to be formally different. The first and most essential thing to do in this situation is to identify the differences between the two sides. It is guaranteed in here that there are only three differences or less between the two sides: functions are different, operations are different, and angles are different. To see what finding the differences means, let's see a couple of examples.
Verify the followings:
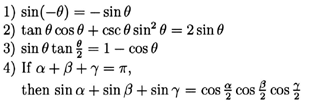
In example 1, there are no differences of functions or operations
because both sides have sine
functions and multiplication operations, if looking 
as the product of 
.
There is a difference of angles since the left side has 
radians and the right side has 
radians. This problem has only difference of angles out of the
three differences that were stated.
In example 2, first of all we see the difference of functions.
The left side has tangent, cosine,
cosecant, and sine
functions while the right side has only the sine
function. Then there is a difference of operations of having addition
on the left side and multiplication on the right. The angles on
both sides are both
radians, so we can say that there is no difference of angles.
This second problem has two out of the three differences that
were stated.
In example 3, there are all kinds of differences. There is difference
of functions since the left side has sine
and tangent functions while the
right side has cosine function.
There is also difference of operations because the left side is
multiplication and the right side is subtraction. Finally, there
is difference of angles. The left side has angles of
and 
radians, and the right side has an angle of
radians. This problem has all three differences that were stated.
In example 4, again we have all kinds of differences. Differences
of functions: sine functions
on left and cosine functions
on right, difference of operations: addition on the left and multiplication
on the right, difference of angles, angles of 
,
,
and 
radians on the left, and angles of 
,
,
and 
on the right. This problem also has all three differences.
From the four examples above, we had an identity with one difference, one with two differences, and two with three differences. There is never going to be an identity with more than three differences, at least not that we know of, and it is very important to keep that in mind. We like to say that the process of verifying an identity is just the process of reducing the three differences between the two sides. It really is the essence of verifying an identity. If all of the differences between the two sides are gone, then the process of verifying the identity is finished.
We know that the process of verifying an identity is also the process of using some basic formulas to transform one side of the identity to another side. The key of using all formulas is good memorizing, and understanding all the formulas.
