[Index]
 |
Sum and Difference Formulas:
There are four possible products of two factors that can be formed
from 
,
,
,
and 
.
Namely: 
,
,
,
.
Note their distribution in the first four formulas. The right
hand sides of (1) and (2) consist of the algebraic sum of
and ,
while (3) and (4) consist of the mixed products. Note the distribution
of signs below.
In formulas 1 and 2, for cosine the signs on each side of the formulas are "opposite". Be aware of the order of the subtraction: the product of cosine minus the product of sine.
In formulas 3 and 4, for sine the
signs on both sides are the same. Be aware of the subtraction
in formula 4: in front of the product is negative, when the product
contains the factor , where 
is from the term of
.
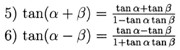
Formulas 5 and 6, tangents have the same sign in
the numerator of both sides. The numerator is also what you get if you multiply tangent by 
(i.e. 
. Notice, this is not actually how it works).
The denominator is 
, the sign being the opposite of the numerator.
