[Index]
 |
Example 5
![]()
Nice to see you here! You are already half way done with our Examples section. There are more complex problems waiting for you. You will learn a lot more from the way we prove them, however. From this example, you will learn our "borrowing" strategy. You will see what it means when we use it.
To prove this identity, we need to compare the two sides of this identity first. We see that it has all three differences.
There are several ways to prove this identity. The first way we will use is our "borrowing" strategy. The idea is: because the two sides are equal, so we believe the left side actually has the factor(s) of the right side. We just don't see them or just see some of them. To reduce the differences, we just want to make both sides the same. To do so, we multiply and divide the left by a factor on the right, which means we are actually multiplying by 1.
For this identity, we multiply the left side by ![]() which is 1, so we are not changing the value of the left
side.
which is 1, so we are not changing the value of the left
side.
![]()
We take out ![]() from the top because we want to keep it, and only modify
from the top because we want to keep it, and only modify ![]() .
We want to show it is equal to
.
We want to show it is equal to ![]() .
To reduce the differences, we reduce the difference of operations
first because
.
To reduce the differences, we reduce the difference of operations
first because ![]() is in multiplication form. By using the Sum
to Product formulas we have:
is in multiplication form. By using the Sum
to Product formulas we have:
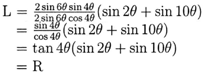
The identity has been proven.
So, did you see how it works? Using the same techniques, we can prove this identity in another way.

