[Index]

	Introduction
	Essence
	Memorizing How to memorize Basic Formulas Sum and Difference Formulas Double & Triple Angle Formulas Half Angle Formulas Product to Sum Formulas Sum to Product Formulas All Formulas
	Understanding Page 1 Page 2 Page 3 Page 4 Page 5
	Summarizing Page 1 Page 2
	Examples Examples Example 1 Example 2 Example 3 Example 4 Example 5 Example 6 Example 7 Example 8 General ideas
	Exercises
	Final thoughts

(10)

Comparing this with the right side of equation (6), the right side has no term of form 2ab, so we want to cancel the term of .

Comparing equations (6) and (9) reminds us of the algebraic formulas , which cancels the middle term 2xy in the perfect squares.

We square equation (9) and add it with equation (10). Because it equals to 0, so we are adding nothing. After combining like terms, we will cancel the terms .

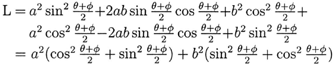
The formula can help us to cancel the angle , we have:

, that is, (6) holds.

Now let's go back to equation (5), we have:

Since ,

The identity has been proven.

So how do you feel now? If necessary, feel free to go back and look at it again.

Actually by using our idea—reduce the differences, we can easily explain why we took each step, even on hard problems. And believe it or not, we have another way to prove this identity. The second way is neither harder nor easier. It will just add more powerful skills to you.