Example 4--Page 3

Still, using our compare strategy, we know should equal to . You can tell that this is not abusive. What is the difference? The operations are different. There are 4 terms in the parenthesis, we should combine them. How could we do that? By combining -1 and we get , which is a like term with another . You might see that , which is one of the Double Angle formulas.

Again, use our compare strategy, should equal to . It’s just the Sum to Product formula.

The identity has been proven.

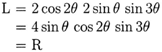
The main idea in proving this problem is to compare both sides often so we will know what's the next step. Always try to get closer to what we want. Once you find out what you need, use formulas to get it. It sounds easy, but try to think about it and make sure you understand what we mean. And think how you can reach your target.