Example 2--Page 2

By using our idea, it's not hard to do the same problems in several ways.

Usually we can choose which difference to reduce first. One way maybe easier than others. Also we could use different formulas.

So here we give you another proof, which is neither easier nor harder than the first proof. In the first proof we try to reduce the difference of angles first, but now we will reduce the difference of operations first. The good thing is we don't need to know the Triple Angle formulas.

To reduce the difference of operation, we combine the two terms at left side to one term.

When you get to here, you might get stuck. What are you going to do? We are trying to reduce the difference of operations. So we want to continue to combine the terms on the top of left. We find that the Sum and Difference formulas can do that.

Then we want to use Double Angle formulas to change to for canceling .

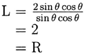
The identity has been proven.

Sometime, when you can't get farther, try to think about what you are trying to get, and think about which formula(s) can help you. Remember, if necessary you can use the formulas from either side.