Invariant Properties of Quadrilaterals

IDevice Icon Quadrilateral of Midpoints

Construct any quadrilateral Q  (not regular)

  1. Locate and join all the midpoints to construct a polygon Q'
  2. Manipulate the quadrilaterals and discuss your obseravtions

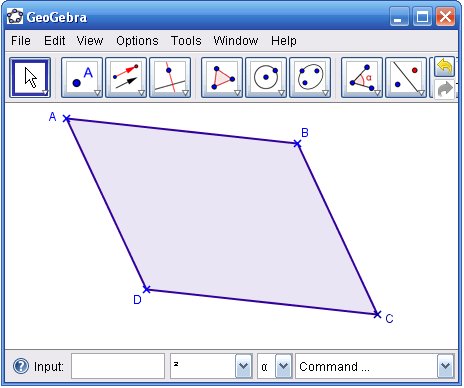
IDevice Icon From Parallelogram to Quadrilateral

  1. Given a parallelogram BADC, construct a quadrilateral PQRS in which D is the midpoint of PQ, C is the midpoint of QR, B is the midpoint of SR and A the midpoint of PS.
  2. Open and use the the file "Para_inv.ggb" or "Para_inv.html" in the above construction


iDevice icon Invariance in Mathematics
  1. Why does the midpoints in a quadrilateral always give a parallelogram?
  2. How many quadrilaterals can you construct from the parallelogram "Para_inv1"?
iDevice icon Justification
« Previous | Next »

Licensed under the GNU Free Documentation License

JCA Presentation: Using GeoGebra in Secondary School Mathematics teaching