|
Light version
|
Essence
Memorizing
Understanding
Summarizing
Examples
Example 1
Example 2
Example 3
Example 4
Example 5
Example 6
Example 7
Example 8
General ideas
Final thoughts
Example 6--Page 2
We want 
.
Looking at the right side we want to get 
from the left side. We know by the Product
to Sum formulas, sine multiplied
by cosine will become sine
plus sine, and 
,
,
;
,
,
.
So we will get
and 
,
but by using the Derived formula,
.
We reach our goal.
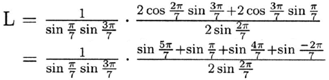
Since 
.
Now for the second factor, we still
didn't reach the goal 
,
and cancel 
.
But we see it is simpler than the last step. Same idea, we want
.
It looks like the Sum to Product
formulas. If we use the Sum
to Product formula of sines
immediately, we have 
.
The right side of it is not 
.
We need ,
not 
!
How can we get ?
If we use the Derived formulas
we have 
,
which is what we want.
The identity has been proven.
This problem is a little bit more difficult than the previous ones. You can see that Derived formulas are very useful for actual angle identities.
