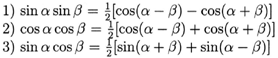
Notice--the sine product and the cosine product have the same cosine expression with one negative and one positive. The cosine product becomes cosine sum, and sine product becomes cosine difference. Note the order of the subtractions: the cosine of the difference of the angles minus the cosine of the sum of the angles. Mixed sine and cosine product gives an all sine answer. The mixed product becomes a sine sum. Be aware of the order of in the term , is the angle of the sine function and is the angle of the cosine function in the mixed product.

Also, we need to memorize that when products go to sums, the angles and become and . Don't forget the coefficient 's in each formula.