[Index]
Introduction
Essence
Memorizing
Understanding
Summarizing
Examples
Exercises
Final thoughts |
4. Understanding the formulas--Page 2
We know the Double-Angle formula of cosine: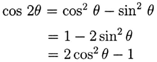
which show us the relationship between angles
and 
.
These three presentations are not different essentially. Using
the formula 
,
we can get one form from other two forms. Now from the idea of
transforming the three differences, we understand how to use these
three formulas. If we want to transform
to
and cosine to sine,
we use the second form. If we want to change
to
and keep the function cosine, we
use the third form, if we want to change
to
and cosine to cosine
and sine we use the first
form.
The Sum to Product formulas are as following:
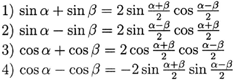
In section
3, we told you how to memorize these four formulas. Of course,
the first role of these formulas is changing sum to product from
the left to the right. Now we need to know what kinds of functions
can transform to the others, and as well as the angles. From the
formulas we see, sine plus
or minus sine changes to
sine times cosine;
cosine plus cosine
to cosine times cosine;
cosine minus cosine
to sine times sine;
and 
,
to
and 
.
We can not explain every formula for you. We believe that you can analyze every formula like we did. After you read our eliciting explanation above, please complete the analysis of all formulas, which is important for you to solve problems.
