[Index]
Basic Formulas
Sum and Difference Formulas
Double & Triple Angle Formulas
Half Angle Formulas
Product to Sum Formulas
Sum to Product Formulas
All Formulas
 |
Sum-to-Product Formulas:
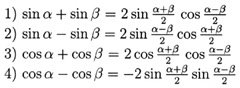
Notice--cosine sums have all cosine
product or all sine product answers
and sine sums have the mixed
products of sine and cosine.
When sums go to products the angles ![]() and
and ![]() become
become ![]() and
and ![]() .
Note the distribution of angles and functions, and what formula
has coefficient -2.
.
Note the distribution of angles and functions, and what formula
has coefficient -2.
![]()
In formulas 1 and 2, be aware the order of functions in the products:
cosine is behind sine.
And the order of angles, sine
plus sine gives the first factor
![]() and the second is
and the second is ![]() .
sine minus sine
makes the first factor
.
sine minus sine
makes the first factor ![]() and the second
and the second ![]() .
.
![]()
In formulas 3 and 4, the sum of cosines of ![]() and
and ![]() become the product of cosines of
become the product of cosines of
![]() and
and
![]() . The
differences of cosines of
. The
differences of cosines of ![]() and
and ![]() become the product of sines of
become the product of sines of ![]() and
and ![]() . Note
. Note ![]() in
in ![]() and
and ![]() have the same order, and the
coefficient is negative 2, which is different from other three formulas.
have the same order, and the
coefficient is negative 2, which is different from other three formulas.
We hope you can memorize all these formulas effectively, because they are really important. After you think you know all of them then go to Understanding the Formulas section to learn more about them. Or if you need more information about the basic trigonometric formulas, then come here for more information. Good luck.

