[Index]
Introduction
Essence
Memorizing
Understanding
Summarizing
Examples
Example 1
Example 2
Example 3
Example 4
Example 5
Example 6
Example 7
Example 8
General ideas
Exercises
Final thoughts
|
Proofs of example 8:
Suppose that a, b, c, 
,
and 
are real numbers, with the following conditions: 
,
,
k is any integer.
 |
(1) |
 |
(2) |
Prove that 
.
First proof:
| (1) + (2) |  |
(3) |
that is, 
Dividing by 2,
 |
(4) |
Squaring the both sides,
 |
(5) |
Claim
 |
(6) |
(1) - (2)  |
(7) |
 |
(8) |
From ,
we have: 
From equation (8), we have:
 |
(9) |
From (6), we have:
 |
(10) |
Squaring (9) and adding it to (10), we have:
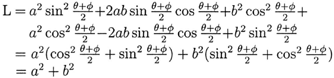
From equations (5) and (6), we have:
Since ,
Second proof:
| From (1) |  |
(3) |
| From (2) |  |
(4) |
where 
satisfies 
,
or 
(if
a = 0).
| (3) + (4) |  |
| that is, |  |
 |
Since ,
Squaring the
both sides,  |
(5) |
|
Claim: |
 |
(6) |
(3) - (4) 
Since ,
that is,
 |
(7) |
Since ,
so 
Since 
,
.
Hence (6) holds. From equations (5) and (6) we have:
