Harmonic Synthesis:
| If a clarinet and a trumpet play the same note, they sound very different from each other. Although they might have the same pitch and the same fundamental frequency (same note, for example, 440 Hz), they don't have the same tone quality. Where the two instruments differ is in harmonics.
Harmonics are tones whose frequencies are integral multiples of the fundamental frequency of the wave. For example, if an A is being played at 440 Hz, the frequencies of the harmonics will be 880 Hz, 1320 Hz, and so on. The harmonics are numbered in order of increasing frequency. Thus, the first harmonic is the fundamental frequency, the second is twice the fundamental frequency, etc. The relative strengths of these harmonics determine the timbre, or quality, of the tone.
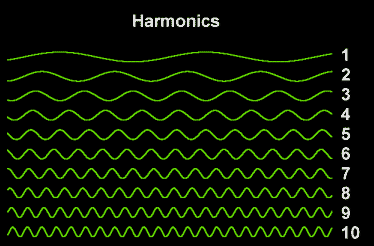 Each instrument is producing harmonics whose relative intensities depend on the type and make of the instrument and how the musician plays it. The graphs of the sound waves for these two instruments are called waveforms. The waveform of a tuner contains no other harmonics, only the fundamental frequency. However, the waveform of the clarinet contains large amounts of the third, fifth, and seventh harmonics, and smaller amounts of the second, fourth, and sixth harmonics, and of course, the first harmonic, the fundamental frequency. The trumpet's waveform consists of a large amount of the third harmonic, and some from the second, fourth, and fifth harmonics, along with the fundamental frequency.
 Harmonic synthesis is the construction of a sound wave from its harmonic components. In order to come as close as possible to the exact waveform of the instrument, more harmonics must be used in the synthesis of the instrument's sound. Electronic music synthesizers use a series of harmonics whose relative amplitudes can be adjusted to fit the desired instrument's waveform. On more advanced synthesizers, they can adjust the attack, decay, vibrato, tremolo, and release of each note. Bands today use synthesizers all the time in their music because the sound they produce is nearly indistinguishable from the real instrument's sound. The reverse of harmonic synthesis is harmonic analysis, where a sound is broken up into it's harmonics. This requires complex math called Fourier analysis, after Jean Baptiste Joseph Fourier, a French mathematician who studied periodic functions.
|

